Kunci Jawaban Matematika Kelas 12 Halaman 25, Uji Kompetensi

TRIBUNNEWS.COM - Berikut kunci jawaban Matematika kelas 12 halaman 25.

Pada buku Matematika Kelas 12 halaman 24 memuat tugas Uji Kompetensi.

Soal pada buku Matematika kelas 12 halaman 25 berisi soal untuk menentukan jarak titik sudut bangun ruang.

Sebelum menengok kunci jawaban Matematika kelas 12 halaman 25 diharapkan siswa mengerjakan soal secara mandiri.

Kunci jawaban Matematika kelas 12 ini diperuntukkan bagi orang tua untuk memandu proses belajar anak.

Tribunnews.com tidak bertanggung jawab dalam perbedaan jawaban pada kunci jawaban Matematika kelas 12 halaman 25.

Baca juga: Kunci Jawaban Matematika Kelas 12 Halaman 24, Soal Latihan 1.3: Jarak Titik Bangun Ruang

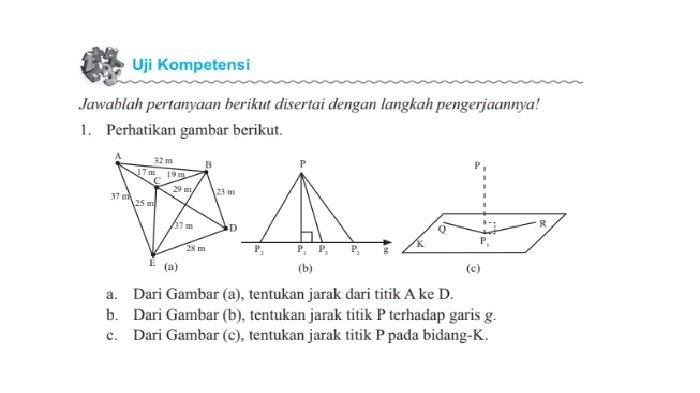
1. Perhatikan gambar berikut.

a. Dari Gambar (a), tentukan jarak dari titik A ke D.
b. Dari Gambar (b), tentukan jarak titik P terhadap garis g.
c. Dari Gambar (c), tentukan jarak titik P pada bidang-K.

Jawaban:

(a) Jarak dari titik A adalah panjang AD
yaitu AC + CD

=17 m +29m
= 46 m

(b) Jarak titik P terhadap garis g adalah panjang PP₁ karena P₁ terletak pada garis g dan PP₁  ⊥ g

(c) Jarak titik P pada bidang-K adalah PP₁ karena P₁ terletak pada garis RP₁
atau garis QP₁ dimana garis RP₁
atau garis QP₁ terletak pada bidang-K
dan PP₁ ⊥ QP₁
atau PP₁ ⊥ RP₁

2. Diketahui kubus ABCD.EFGH dengan panjang rusuk 9 cm. Buat ilustrasi kubus tersebut. Tentukan langkah menentukan jarak titik F ke bidang BEG. Kemudian hitunglah jarak titik F ke bidang BEG.

Jawaban:

Kubus dengan rusuk a cm.
Panjang diagonal Sisi = a√2 cm
Panjang diagonal ruang = a√3 cm

Contoh diagonal Sisi
Sisi alas = AC dan BD
Sisi belakang = CH dan DG
dan seterusnya

Contoh diagonal ruang
AG, HB, DF dan CE

Langkah — langkah

1) Buat kubus ABCD.EFGH dengan rusuk 9 cm
2) Buat segitiga BEG dan buat garis tinggi segitlga BEG yaitu OB dengan O titik tengah EG
3) Jarak F ke BDG sama dengan jarak F ke garis OB
4) Buat segitiga BFO siku-siku di F
5) Tentukan ukuran sisi-sisi segitiga BFO tersebut
FB = 9 cm => rusuk kubus
FO = 1/2 HF = 1/2 (9√2) = (9/2)√2cm
dengan phytagoras
OB = √(FB² + FO²)
OB = √(9² + (9/2√2)²)
OB = √(81 + 81/4 . 2)
OB = √(324/3 + 162/4)
OB = √(486/4)
OB = √(81/4 . 6)
OB = (9/2)√6cm

6) Pada segitiga BFO
Jika alasnya FO maka tingginya FB
Jika alasnya OB maka tingginya jarak F ke OB = t
dengan kesamaan luas segitiga (1/2 x alas x tinggi)
1/2 x OB x t = 1/2 x FO x B
OB x t = FO x FB
t = (FO x FB) /OB
t = ((9/2)√2 x 9) / (9/2)√6
t = (9√2)/√6
t = 9√3 / 3
t = 3√3

Jadi jarak F ke BEG = 3√3cm

Cara cepat:
Jarak F ke BEG
= 1/3 x diagonal ruang DF
= 1/3 x 9√3 cm
= 3√3 cm

Baca juga: Kunci Jawaban Bahasa Inggris Kelas 12 Halaman 98, Listening Comprehension Task 4

3. Diketahui kubus ABCD.EFGH dengan panjang rusuk a. Jika titik P terletak pada perpanjangan AB sehingga PB = 2a, dan titik Q pada perpanjangan FG sehingga QG = a.

a. Buatlah ilustrasi dari masalah di atas.
b. Tentukan PQ.

Jawaban:

Jarak P ke Q adalah PQ
BP = 2a dan GQ = a
segitiga BPR siku di B, maka,
PR² = BP² + BR²
= (2a)² + (2a)²
= 8a²
PR = 2a√2

RQ = panjang rusuk = a
Segitiga PQR siku di R, maka
PQ² = PR² + QR²
= (2a√2)² + a²
= 8a² + a²
= 9a²
PQ = 3a

4. Panjang setiap bidang empat beraturan T.ABC sama dengan 16 cm. Jika P pertengahan AT dan Q pertengahan BC, tentukan PQ.

Jawaban:

Karena merupakan bidang 4 beraturan maka berbentuk limas segitiga dengan setiap bidangnya merupakan segitjga sama sisi dengan panjang sisinya 16 cm
AB = BC = AC = AT = BT = CT = 16 cm

p titik tengah AT maka AP = TP = 8 cm
Q titik tengah BC maka BQ = CQ = 8 cm

Untuk menentukan panjang PQ kita buat segitiga AQT
AT = 16 cm rusuk limas

AQ = √(AB² - BQ²)
AQ = √(16² - 8²)
AQ = √(256 - 64)
AQ = √192
AQ = √64 X √3
AQ = 8√3 cm

QT = √(TB² - BQ²)
QT = √16² - 8²)
QT = √(256 - 64)
QT = √(192)
QT = 8√3

karena QT = AQ maka segitiga AQT adalah segitiga sama kaki
PQ adalah tinggi segitiga AQT dengan alas AT

PQ = √(AQ² - AP²)
PQ = √((8√3)² - 8²)
PQ = √(192 - 64)
PQ = √128
PQ = √64 X √2
PQ =  8√2 cm

Cara cepat mencari tinggi segitiga sama sisi dengan sisi a cm adalah
t=1/2 x a√3

Jadi AQ dan QT adalah tinggi segitjga sama sisi dengan sisi 16 cm
= 1/2 x 16√3
= 8√3 cm

5. Perhatikan gambar kubus ABCD.EFGH. Tentukan jarak titik H ke DF.

Jawaban:

ΔDHF siku-siku di H
Buat T pada DF sehingga HT tegak lurus dengan DF
HT = jarak H ke DF

DH = 6
DH = 6√3
HF = 6√2

HT . DF = DH . HF
HT (6√3) = 6(6√2)
HT = 6(6√2) / 6√3
HT = 2√6

(Tribunnews.com/Enggar Kusuma)