Kunci Jawaban Matematika Kelas 8 Halaman 124 125: Cara Tentukan Korespondensi Satu-Satu

TRIBUNNEWS.COM - Berikut adalah kunci jawaban Matematika Kelas 8 halaman 124 125 soal ayo kita berlatih 3.4 cara menentukan korespondensi satu-satu.

Buku Matematika kelas 8 semester 1 adalah buku implementasi Kurikulum 2013 edisi revisi 2017.

Buku Matematika Kelas 8 SMP/MTs merupakan karya dari Abdur Rahman As’ari, Mohammad Tohir, Erik Valentino, Zainul Imron, Ibnu Taufiq.

Artikel berikut akan memuat kunci jawaban ayo kita berlatih 3.4 cara menentukan korespondensi satu-satu di halaman 124 125.

Kunci jawaban Buku Matematika Kelas 8 ini dapat ditujukan kepada orang tua atau wali untuk mengoreksi hasil belajar.

Sebelum menengok hasil kunci jawaban pastikan siswa harus terlebih dahulu menjawab soal yang disiapkan.

Baca juga: Kunci Jawaban Matematika Kelas 8 Halaman 64, Cara Tentukan Posisi Titik Terhadap Sumbu X dan Sumbu Y

Lalu gunakan artikel ini untuk mengoreksi hasil pekerjaan siswa.

Kunci jawaban Buku Matematika Kelas 8 halaman 124 125

Soal Ayo Kita Berlatih 3.4

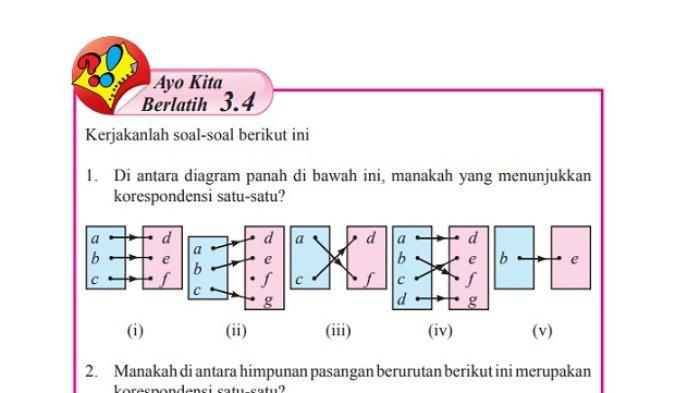
Soal nomor 1

Dari diagram panah tersebut yang menunjukan korespondensi satu-satu adalah nomor (iii), (iv), dan (v).

Soal nomor 2

Himpunan pasangan berurutan yang merupakan korespondensi satu-satu adalah:

C. {(5,6), (6,7), (7,5)}

D. {(1,1), (2,2), (3,3)}

F. {(a,2), (2,b), (b,a)}

Soal nomor 3

a. Jumlah semua korespondensi satu-satu yang mungkin terjadi dari P ke Q adalah 720.

b. 1. {(1, a), (2, b), (3, c), (4, d), (5, e), (6, f)}

2. {(1, b), (2, a), (3, c), (4, d), (5, e), (6, f)}

3. {(1, a), (2, b), (3, f), (4, d), (5, e), (6, c)}

Soal nomor 4

a. f : x -> -X

Soal nomor 5

Kemungkinan yang terjadi adalah:

a.Berikut gambar diagaram panah yang menunjukan korespondensi satu -satu dari K ke L:

Baca juga: Kunci Jawaban Matematika Kelas 8 Halaman 86 87: Cara Membuat Bentuk Penyajian Relasi dengan Benar

K = {merah, kuning, hijau} dan
L = {∠A, ∠B, ∠C}

b. Banyak korespondensi satu -satu yang terjadi sebanyak 6

Soal nomor 6

a. Jika diketahui A = {faktor dari 8} adalah (1 × 8) dan (2 × 4)

Maka:
A = {1, 2, 4, 8} sehingga n(A) = 4

dan
B = {faktor dari 21} adalah (1 × 21) dan (3 × 7)
Maka:
B = {1, 3, 7, 21} sehingga n(B) = 4

Sehingga n(A) = n(B) = 4, jadi banyak korespondensi satu-satu yang bisa dibuat adalah = 4 × 3 × 2 × 1 = 24.

b. Jika diketahui P = {huruf fokal}

Maka:
P = {a, e, i, o, u} sehingga n(P) = 5

dan
Q = {bilangan cacah antara 1 dan 7}
maka:
Q = {2, 3, 4, 5, 6} sehingga n(Q) = 5

Sehingga n(P) = n(Q) = 5, jadi banyak korespondensi satu-satu yang bisa dibuat adalah = 5 × 4 × 3 × 2 × 1 = 120

Soal nomor 7

a. Banyak korespondensi satu-satu yang bisa dibuat adalah 9

b. Banyak korespondensi satu-satu yang bisa dibuat adalah 12

Soal nomor 8

- Sekolah dengan murid

- Rel dengan Kereta

- Negara dengan ibukota negara

- Sepak bola dengan bola

- Bandara dengan pesawat

*) Disclaimer: Artikel ini hanya ditujukan kepada orangtua untuk memandu proses belajar anak.

Sebelum melihat kunci jawaban, siswa harus terlebih dahulu menjawabnya sendiri, setelah itu gunakan artikel ini untuk mengoreksi hasil pekerjaan siswa.

(Tribunnews.com/ Muhammad Alvian Fakka)