Kunci Jawaban Matematika Kelas 12 Halaman 207 dan 212: Contoh Soal 4.2.2 dan 4.2.3

TRIBUNNEWS.COM - Berikut kunci jawaban Matematika kelas 12 semester 2 halaman 207 dan 212.

Pada Buku Matematika kelas 12 terdapat Contoh Soal 4.2.2 dan 4.23.

Jawaban dari soal tersebut akan dibahas di bawah ini, tetapi ada baiknya siswa tidak menjadikan artikel ini sebagai acuan.

Siswa lebih baik mencoba menjawab sendiri terlebih dahulu dengan bantuan orangtua.

Kunci jawaban soal Matematika kelas 12 halaman 207 dan 212 semester 2 Contoh Soal 4.2.2 dan 4.2.3.

Contoh soal 4.2.2

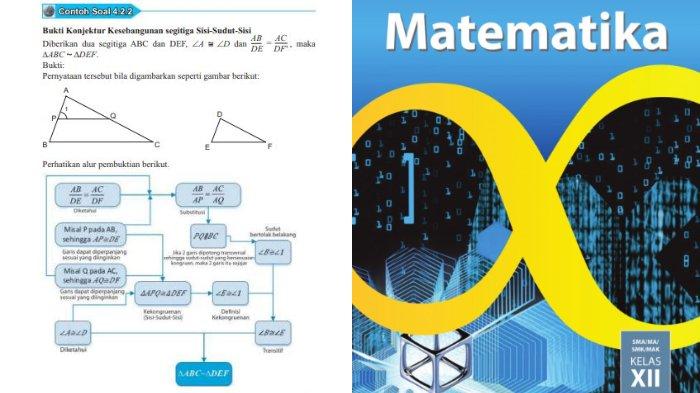
Buktikan Konjektur Kesebangunan segitiga Sisi-Sudut-Sisi

Diberikan dua segitiga ABC dan DEF, ∠A ≅ ∠D dan AB/DE = AC/DF, maka ∆ABC ~ ∆DEF.

Pembuktian:

Pernyataan tersebut bila digambarkan seperti berikut:

Diketahui: ∠A ≅ ∠D dan AB/DE = AC/DF

Akan dibuktikan: ∆ABC ~ ∆DEF

Bukti Formal: (lengkapi bagian alasan yang mendukung pernyataan-pernyataannya).

1.     Misal P adalah titik AB, sehingga AP ≅ DE (sisi) : Garis bisa diperpanjang sesuai dengan keinginan

2.     Misal Q adalah titik pada AC, sehingga AQ ≅ DF (sisi) : Garis bisa diperpanjang sesuai dengan keinginan

3.     ∠A ≅ ∠D (sudut) : Diketahui

4.     ∆APQ ≅ ∆DEF : Konjektur Kekongruenan (Sisi-Sudut-Sisi)

5.     ∠E ≅ ∠I : Definisi kekongruenan segibanyak

6.     AB/DE = AC/DF : Diketahui

7.     AB/AP = AC/AQ : Subtitusi

8.     PQ || BC : Jika 2 garis dipotong transversal sehingga sudut-sudut yang bersesuaian kongruen, maka 2 garis itu sejajar

9.     ∠B ≅ ∠I : Sudut bertolakbelakang

10. ∠B ≅ ∠E : Sifat transitif

11. ∆∠ABC ~ ∆∠DEF : Konjektur Sudut-Sudut

Baca juga: Kunci Jawaban Matematika Kelas 12 Halaman 231 Semester 2: Uji Kompetensi Nomor 1-4 Tentang Kongruen

Contoh soal 4.2.3

Bukti Konjektur Kesebangunan segitiga Sisi-Sisi-Sisi

Diberikan dua segitiga ABC dan DEF, di mana AB/DE = AC/DF = BC=EF, maka ∆ABC ~ ∆DEF.

Pembuktian:

Untuk mempermudah proses berpikir dalam penulisan pembuktian secara deduktif, perhatikan alur berpikir berikut ini:

Berdasarkan alur pembuktian di atas, lengkapi pembuktian formal berikut ini:

Diketahui: AB/DE = AC=DF = BC/EF

Akan dibuktikan ∆ABC ~ ∆DEF.

1.      Misal P pada AB, sehingga AP ≅ DE : Garis bisa diperpanjang sesuai yang diinginkan

2.      Misal Q pada AC, sehingga AQ ≅ DF : Garis bisa diperpanjang sesuai dengan keinginan

3.      AB/DE = AC/DF : Diketahui

4.      AB/AP = AC/AQ : Subtitusi

5.      PQ || BC : Jika 2 garis dipotong transversal sehingga sudut-sudut yang bersesuaian kongruen, maka 2 garis itu sejajar

6.      ∠B ≅ ∠1 dan ∠C ≅ ∠2: Sudut Sehadap

7.      ∆ABC ≅ ∆APQ: Konjektur Kesebangunan Sudut-Sudut

8.      AB/AP = BC/PQ : Definisi Kesebangunan Segibanyak

9.      AB/DE = AC/DF = BC/EF : Diketahui

10.   PQ = EF : Subtitusi

11.  ∆APQ ≅ ∆DEF : Konjektur Kekongruenan segitiga

12.  ∠B ≅ ∠E dan ∠C ≅ ∠F : Definisi Kekongruenan dan subtitusi

13.  ∆ABC ~ ∆DEF : Konjektur Kesebangunan segitiga Sudut-Sudut.

*) Disclaimer: Jawaban di atas hanya digunakan untuk memandu proses belajar anak.

Sebelum melihat kunci jawaban, siswa harus terlebih dahulu menjawabnya sendiri, setelah itu gunakan artikel ini untuk mengoreksi hasil pekerjaan siswa.

(Tribunnews.com/Isti Prasetya)